Introductory test for the course Control Systems for Smart Agriculture
Second order ODE
Given the second order ODE
$$\ddot{y}\left(t\right) = -k \sin\left(y\left(t\right)\right) – c\dot{y}\left(t\right) + M\left(t\right)$$
where \(M\left(t\right)\) is the forcing input, find a suitable choice of state variables and write the system in state space form.
Selecting as state variables
$$\begin{aligned} x_1(t) &= y(t)\\ x_2(t) &= \dot{y}(t) \end{aligned}$$
the system can be written in state space form as
$$\begin{aligned} \dot{x}_1(t) &= x_2(t)\\ \dot{x}_2(t) &= -k \sin\left(x_1(t)\right) – c x_2 + M(t) \end{aligned}$$
Equilibrium
For the second order system in state space form
$$\begin{aligned} \dot{x}_1(t) &= x_2(t)\\ \dot{x}_2(t) &= -k\sin(x_1(t))-c x_2(t) + M(t) \end{aligned}$$
verify that the pair \(\bar{x}_1 = 0\), \(\bar{x}_2 = 0\) is an equilibrium with input \(M(t) = \bar{M} = 0\).
The equilibrium conditions for this system are
$$\begin{aligned} 0 &= \bar{x}_2 \\ 0 &= -k\sin(\bar{x}_1)-c\bar{x}_2+\bar{M} \end{aligned}$$
which are satisfied by \(\bar{x}_1 = 0\), \(\bar{x}_2 = 0\), \(\bar{M} = 0\).
Linearisation
For the second order system in state space form
$$\begin{aligned} \dot{x}_1(t) &= x_2(t)\\ \dot{x}_2(t) &= -k\sin(x_1(t))-c x_2(t) + M(t) \end{aligned}$$
compute a linearised model in the neighborhood of \(\bar{x}_1 = 0\), \(\bar{x}_2 = 0\), \(\bar{M} = 0\).
Defining the state variables for the linearised system as
$$\begin{aligned} \delta x_1(t) &= x_1(t)-\bar{x}_1 \\ \delta x_2(t) &= x_2(t)-\bar{x}_2 \\ \delta M(t) &= M(t)-\bar{M} \end{aligned}$$
the linearised system is given by
$$\begin{aligned} \dot{\delta x}_1(t) &= \delta x_2(t)\\ \dot{\delta x}_2(t) &= -k\cos(\bar{x}_1)\delta x_1(t)-c\delta x_2(t)+\delta M(t) = -k\delta x_1(t)-c\delta x_2(t)+\delta M(t) \end{aligned}$$
Linear Time-Invariant continuous-time systems in state space form
Consider the second order LTI system in state space form
$$\begin{aligned} \dot{x}_1(t) &= x_2(t)\\ \dot{x}_2(t) &= -k x_1(t)-c x_2(t) + M(t) \end{aligned}$$
and write it in the standard form
$$\dot{x}(t)=A x(t)+B u(t)$$
with suitable definitions of \(x\) and \(u\), and of matrices \(A\) and \(B\).
Defining the state and input variables as
$$x(t)=\begin{bmatrix} x_1(t)\\ x_2(t)\end{bmatrix}\qquad u(t)=M(t)$$
the system can be written in standard form with matrices
$$A=\begin{bmatrix} 0 & 1\\ -k & -c \end{bmatrix}\qquad B=\begin{bmatrix} 0\\ 1 \end{bmatrix}$$
Stability analysis for Linear Time-Invariant continuous-time systems
For the second order LTI system in state space form
$$\begin{aligned} \dot{x}_1(t) &= x_2(t)\\ \dot{x}_2(t) &= -k x_1(t)-c x_2(t) + u(t) \end{aligned}$$
find conditions on \(k\) and \(c\) under which the system is asymptotically stable.
To check the stability of a LTI system we have to determine the eigenvalues of matrix \(A\), or analyze the characteristic polynomial of matrix \(A\).
The characteristic polynomial of matrix \(A\) is given by
$$\text{det}\left(\lambda I-A\right)=\text{det}\left(\begin{bmatrix} \lambda & -1\\ k & \lambda+c\end{bmatrix}\right)=\lambda^2+c\lambda+k$$
According to the necessary and sufficient condition, the system is asymptotically stable iff \(c>0\) and \(k>0\).
Free response of Linear Time-Invariant continuous-time systems
For the second order LTI system in state space form
$$\begin{aligned} \dot{x}_1(t) &= x_2(t)\\ \dot{x}_2(t) &= -2 x_2(t) + u(t) \end{aligned}$$
compute the free response (\(u(t) = 0\)), starting from the initial condition \(x_1 (0) = 1\) and \(x_2 (0) = 2\).
The free response of the system is given by
$$x(t)=e^{At}x(0)=e^{At}\begin{bmatrix}1\\ 2\end{bmatrix}$$
Transfer function of Linear Time-Invariant continuous-time systems
For the second order LTI system in state space form
$$\begin{aligned} \dot{x}_1(t) &= x_2(t)\\ \dot{x}_2(t) &= -k x_1(t) -c x_2(t) + u(t)\\ y(t) &= x_1(t) \end{aligned}$$
compute the transfer function from input \(u\) to output \(y\) and evaluate its poles, zeros and gain.
Applying the Laplace transform to each equation we obtain
$$\begin{aligned} s X_1(s) &= X_2(s)\\ s X_2(s) &= -k X_1(s) -c X_2(s) + U(s)\\ Y(s) &= X_1(s) \end{aligned}$$
Solving with respect to the state variables we obtain
$$\begin{aligned} X_2(s) &= s X_1(s)\\ X_1(s) &= \frac{U(s)}{s^2+cs+k}\\ Y(s) &= X_1(s) \end{aligned}$$
and finally the transfer function is given by
$$Y(s)=\frac{1}{s^2+cs+k}U(s)$$
This transfer function has gain \(\frac{1}{k}\), no zeros, and two poles that are the roots of polynomial \(s^2+cs+k\).
Time response of Linear Time-Invariant continuous-time systems
For the second order system described by the transfer function
$$G(s)=\frac{1}{s^2+cs+k}$$
with \(k = 1\) and \(c = 2\), compute the time response of output \(y\) to the forcing input \(u(t) = \text{step}(t)\).
The response to the forcing input in the Laplace domain, decomposed using Heaviside technique, is given by
$$\begin{aligned} Y(s) &= G(s)\frac{1}{s}=\frac{1}{s(s+1)^2}=\frac{A}{s}+\frac{B}{s+1}+\frac{C}{(s+1)^2}\\ &= \frac{(A+B)s^2+(2A+B+C)s+A}{s(s+1)^2} \end{aligned}$$
Imposing the equivalence between the polynomials at the numerator we obtain
$$\begin{aligned} A+B &= 0\\ 2A+B+C &= 0\\ A &= 1 \end{aligned}$$
Finally, applying the inverse Laplace transfor we obtain
$$y(t)=1-e^{-t}-te^{-t}\qquad t\geq 0$$
Frequency response function of Linear Time-Invariant continuous-time systems
For the second order system described by the transfer function
$$G(s)=\frac{1}{s^2+cs+k}$$
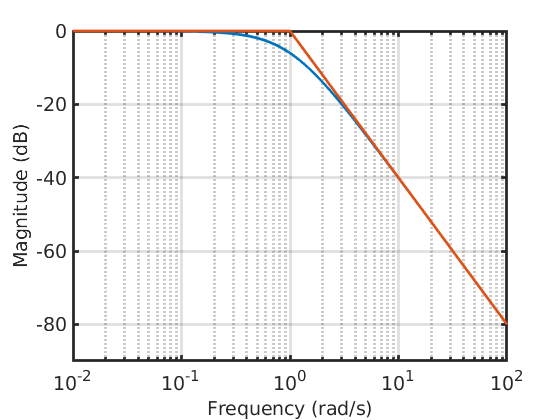
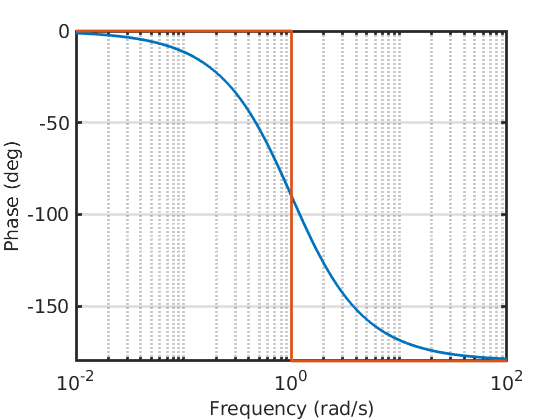
with \(k = 1\) and \(c = 2\), draw the asymptotic magnitude and phase plots of the frequency response function.
Frequency response function of Linear Time-Invariant continuous-time systems
For the second order system described by the transfer function
$$G(s)=\frac{1}{s^2+cs+k}$$
with \(k = 1\) and \(c = 2\), use the asymptotic magnitude and phase plots of the frequency response function to evaluate the amplitude and the phase of the steady-state response of output \(y\) to the input \(u(t) = \sin(0.01t)\).
The system is asymptotically stable, we can thus apply the frequency response theorem to compute the steady-state response to the sinusoidal input.
The amplitude and the phase of the steady-state response are
$$\left|G(j0.01)\right|\approx 1\qquad\angle G(j0.01)\approx 0^\circ$$
The steady-state response is thus given by
$$y(t)\approx\sin(0.01t)$$
Frequency domain design of a continuous time control system
Consider the following control system
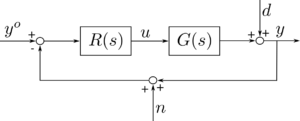
where $$G(s)=10\frac{1+s}{(1+0.1s)^2}e^{-0.5s}$$.
Design the transfer function \(R (s)\) of the controller in such a way that:
- \(e_\infty=0\) for \(y^o(t)=A\,\text{step}(t)\), where \(A\) is an arbitrary real constant, and \(d(t) = n(t) = 0\);
- a disturbance \(d(t) = D\, \sin (\omega_D t)\), where \(D\) is an arbitrary real constant and \(\omega_D \leq 0.03\, \text{rad/s}\), is attenuated on the output of 100 times;
- a disturbance \(n(t) = N\, \sin (\omega_N t)\), where \(N\) is an arbitrary real constant and \(\omega_N \geq 30 \,\text{rad/s}\), is attenuated on the output of 100 times;
- \(\omega_c \geq 1\, \text{rad/s}\) and \(\varphi_m \geq 50^\circ\) ;
- the controller has at maximum order three.
We start from the steady-state design, considering the gain and type of the controller transfer function.
The steady-state error due to the reference signal, when \(d(t) = n(t) = 0\), is given by
$$e_\infty=\lim_{s\rightarrow 0} s\cfrac{1}{1+L\left(s\right)}\cfrac{A}{s}=\lim_{s\rightarrow 0} \cfrac{A}{1+\cfrac{10\mu_R}{s^{g_R}}}=\lim_{s\rightarrow 0} \cfrac{As^{g_R}}{s^{g_R}+10\mu_R}$$
where \(\mu_R\) and \(g_R\) are the gain and type of the regulator, respectively. In order to have a zero steady-state error we must select \(g_R=1\), independently of the value of \(\mu_R\) and \(A\).
The steady-state design can be thus concluded with
$$R_1\left(s\right)=\frac{1}{s}$$
The transient design, instead, starts with the following loop transfer function
$$L_1\left(s\right)=\frac{10}{s}\cfrac{1+s}{\left(1+0.1s\right)^2}e^{-0.5s}$$
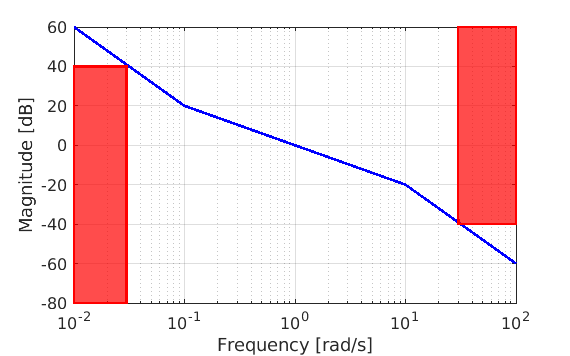
whose magnitude Bode diagram is shown in the following picture.
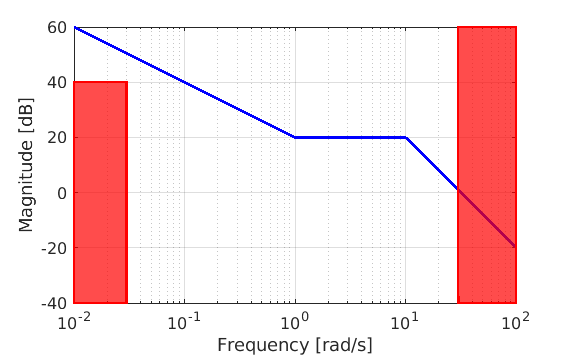
In order to satisfy the constraints on the attenuation of the disturbances \(d\left(t\right)\) and \(n\left(t\right)\) we must have
$$\frac{1}{\left|1+L\left(j\omega\right)\right|}\leq 0.01\qquad\textrm{for}\qquad\omega\leq 0.03\,\text{rad/s}$$
and
$$\frac{\left|L\left(j\omega\right)\right|}{\left|1+L\left(j\omega\right)\right|}\leq 0.01\qquad\textrm{for}\qquad\omega\geq 30\,\text{rad/s}$$
These two constraints can be approximated as
$$\left|L\left(j\omega\right)\right|_{\text{dB}}\geq 40\,\text{dB}\qquad\textrm{for}\qquad\omega\leq 0.03\,\text{rad/s}$$
and
$$\left|L\left(j\omega\right)\right|_{\text{dB}}\leq -40\,\text{dB}\qquad\textrm{for}\qquad\omega\geq 30\,\text{rad/s}$$
A new loop transfer function \(L\left(s\right)\) can be shaped (see the following picture) having the following expression
$$L\left(s\right)=\frac{10}{s}\cfrac{1+10s}{\left(1+100s\right)\left(1+0.1s\right)}e^{-0.5s}$$
and characterised by \(\omega_c\approx 1\,\text{rad/s}\) and \(\varphi_m\approx 50.5^\circ\), that satisfies the requirements.
The corresponding regulator transfer function is
$$R\left(s\right)=\frac{L\left(s\right)}{G\left(s\right)}=\frac{\left(1+10s\right)\left(1+0.1s\right)}{s\left(1+100s\right)\left(1+s\right)}$$
Discretisation of a continuous time control system
Consider the following control system

where
$$G(s)=10\frac{1+s}{(1+0.1s)^2}e^{-0.5s}\qquad R(s)=\frac{\left(1+10s\right)\left(1+0.1s\right)}{s\left(1+100s\right)\left(1+s\right)}$$.
Select a sampling time \(T_s\) for the discretisation of the regulator, in such a way that the decrement in phase margin is less or equal to \(3^\circ\), and compute the digital transfer function corresponding to \(R (s)\) using Backward Euler transformation.
Write the pseudo-code to implement the regulator with transfer function \(R (z)\).
The crossover frequency is approximately equal to \(1\,\text{rad/s}\).
We can select the sampling time according to the relation
$$\omega_c\frac{T_s}{2}\frac{180^\circ}{\pi}=3^\circ$$
approximately equal to \(0.1\,\text{s}\).
The digital transfer function \(R\left(z\right)\) can be computed applying the relation
$$s=\frac{z-1}{T_s z}$$
and obtaining
$$R\left(z\right)=\frac{T_s z}{z-1}\frac{\left[\left(T_s+0.1\right)z-0.1\right]\left[\left(T_s+10\right)z-10\right]}{\left[\left(T_s+1\right)z-1\right]\left[\left(T_s+100\right)z-100\right]}=\frac{0.002 z^3-0.003 z^2+0.001 z}{z^3-2.9 z^2+2.8 z-0.9}$$
The regulator transfer function can be equivalently rewritten as
$$R\left(z\right)=\frac{U\left(z\right)}{E\left(z\right)}=\frac{0.002-0.003 z^{-1}+0.001 z^{-2}}{1-2.9 z^{-1}+2.8 z^{-2}-0.9 z^{-3}}$$
and translated into a difference equation
$$u\left(k\right)=2.9 u\left(k-1\right)-2.8 u\left(k-2\right)+0.9 u\left(k-3\right)+0.002 e\left(k\right)-0.003 e\left(k-1\right)+0.001 e\left(k-2\right)$$
The control algorithm is shown in the following picture.
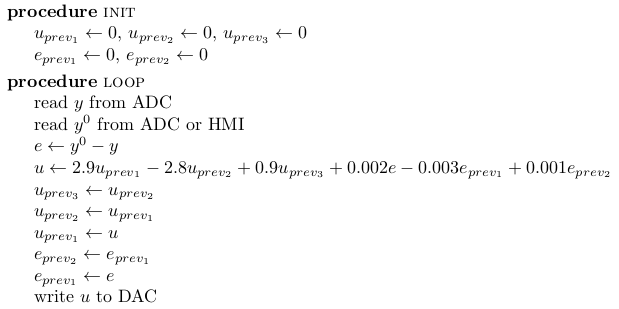
A passive low-pass filter
Compute the transfer function from \(v_{in}\) to \(v_{out}\) of the circuit shown in the picture below.
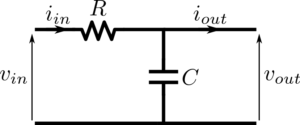
Assume \(i_{in}\) is an arbitrary current and \(i_{out}=0\).
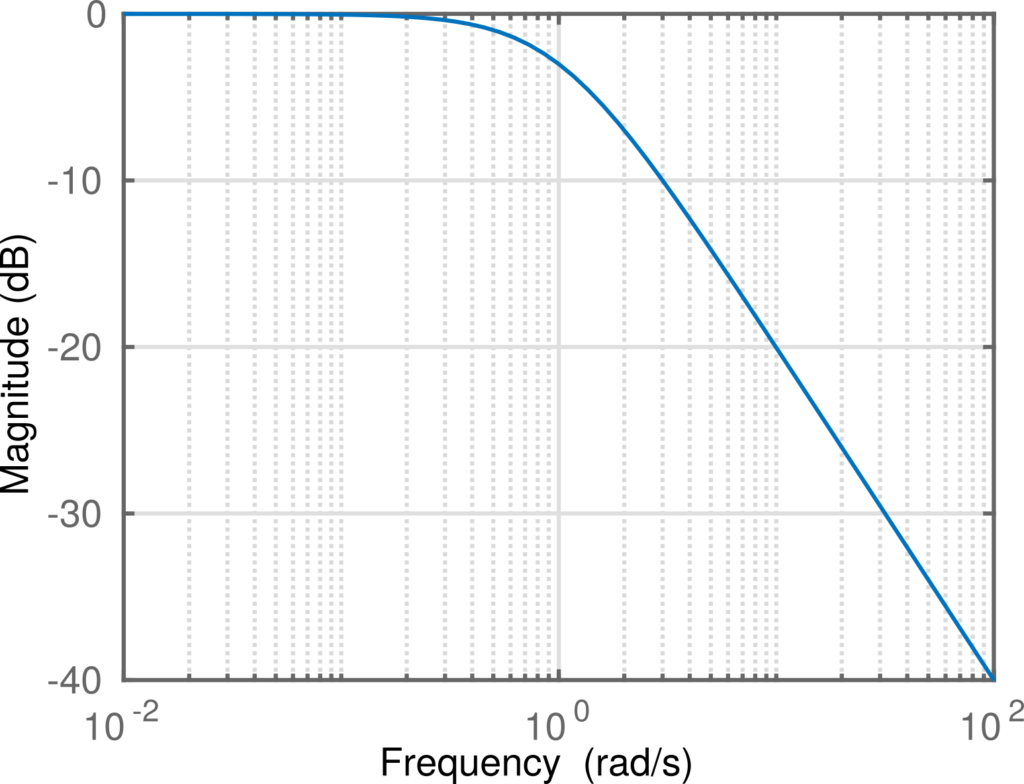
Draw the magnitude Bode diagram of the previous transfer function.
Looking at the loop we can write
$$v_{in}=Ri_{in}+v_{out}$$
and the relation between \(i_{in}\) and \(v_{out}\) is given by
$$i_{in}=C\frac{\mathrm{d}v_{out}}{\mathrm{d}t}$$
Merging these two relations, we obtain
$$\frac{v_{in}-v_{out}}{R}=C\frac{\mathrm{d}v_{out}}{\mathrm{d}t}$$
or equivalently
$$v_{in}=v_{out}+RC\frac{\mathrm{d}v_{out}}{\mathrm{d}t}$$
Applying now the Laplace transform to the previous relation we obtain
$$V_{in}\left(s\right)=\left(1+sRC\right) V_{out}\left(s\right)$$
and thus
$$G\left(s\right)=\frac{V_{out}\left(s\right)}{V_{in}\left(s\right)}=\frac{1}{1+sRC}$$
The following picture shows the magnitude Bode diagram of \(G\left(s\right)\) for \(RC=1\).
The Wheatstone bridge
Consider the circuit in the picture below (Wheatstone bridge), and answer to the following questions:
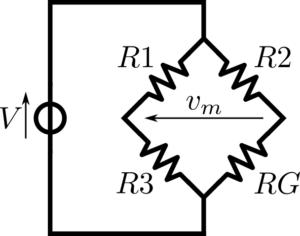
- determine the expression of voltage \(v_m\);
- determine the value \(\bar{R}_G\) of resistor \(R_G\) for which \(v_m=0\) independently of the value of \(V\);
- assuming now resistor \(R_G\) has a resistance \(\bar{R}_G+\Delta R_G\), with \(\Delta R_G\ll\bar{R}_G\), determine the expression of voltage \(v_m\).
Applying Kirchhoff’s rules to the circuit in the picture below
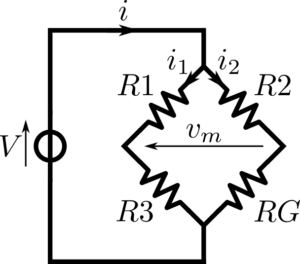
we can write two loop equations and one junction equation
$$\begin{align*}
i &= i_1+i_2\\
V &= \left(R_1+R_3\right) i_1\\
V &= \left(R_2+R_G\right) i_2
\end{align*}$$
From the two last relations we can derive the expressions of \(i_1\) and \(i_2\), as follows
$$i_1=\frac{V}{R_1+R_3}\qquad i_2=\frac{V}{R_2+R_G}$$
and substituting in the first equation
$$i=\left(\frac{1}{R_1+R_3}+\frac{1}{R_2+R_G}\right)V$$
Finally, looking at the loop formed by \(R_1\), \(R_2\) and \(v_m\), we obtain the expression of \(v_m\)
$$v_m=R_2 i_2-R_1 i_1=\left(\frac{R_2}{R_2+R_G}-\frac{R_1}{R_1+R_3}\right)V$$
To determine the value of \(\bar{R}_G\), we have to impose
$$\frac{R_2}{R_2+\bar{R}_G}=\frac{R_1}{R_1+R_3}$$
Solving this relation with respect to \(\bar{R}_G\) we obtain
$$\bar{R}_G=\frac{R_2 R_3}{R_1}$$
Assuming now \(R_G=\bar{R}_G+\Delta R_G\), the expression of \(v_m\) becomes
$$\begin{align*} v_m &=\left(\frac{R_2}{R_2+\bar{R}_G+\Delta R_G}-\frac{R_1}{R_1+R_3}\right)V=\frac{R_2 R_1+R_2 R_3-R_2 R_1-R_2 R_3- R_1\Delta R_G}{\left(R_2+\bar{R}_G+\Delta R_G\right)\left(R_1+R_3\right)}V\\
&=-\frac{ R_1\Delta R_G}{\left(R_2+\bar{R}_G+\Delta R_G\right)\left(R_1+R_3\right)}V \end{align*}$$
If \(\Delta R_G\ll\bar{R}_G\) we can simplify the previous relation as follows
$$v_m=-\frac{ R_1\Delta R_G}{\left(R_2+\frac{R_2 R_3}{R_1}\right)\left(R_1+R_3\right)}V=-\frac{R_1^2}{R_2\left(R_1+R_3\right)^2}\Delta R_G v$$