Introductory test for the course Mathematical Analysis II
Question #1
- \(a\geq1\) and \(b\geq1\);
- \(a\geq1\) or \(b\geq1\);
- \(a>0\) and \(b>0\);
- \(a\neq0\) and \(b\neq0\);
- no answer is correct.
Question #2
- if and only if \(x>1\);
- for any \(x\in\mathbb{R}\);
- never;
- if and only if \(x<1\);
- no answer is correct.
Question #3
Let \(\alpha, \beta \in \mathbb{R}\), with \(\alpha < \beta < 0\). Then, surely
- \(\log |\alpha| > \log |\beta|\);
- \(\tan \alpha > \tan \beta\);
- \(\tan \alpha < \tan \beta\);
- \(\alpha ^2 < \beta ^2\);
- no answer is correct.
Question #4
- \(1\) solution;
- \(2\) solutions;
- \(3\) solutions;
- more then \(3\) solutions;
- no solutions.
Question #5
- \(x-y+z=1\);
- \(x-y+z=0\);
- \(x=1\);
- \((x-1)+(y+1)+(z-1)=1\);
- no answer is correct.
Question #6
The equation $$\ x^2+y^2+y=0$$ describes in the plane
- the circle with radius \(1\) and center \((0,-1)\);
- the circle with radius \(\frac12\) and center \(\big(0,-\frac12\big)\);
- the point \((0,-1)\);
- an hyperbole;
- no answer is correct.
The circle with radius \(\frac12\) and center \(\big(0,-\frac12\big)\)
Question #7
- \(4\) solutions;
- no solution;
- \(2\) solutions;
- \(1\) solution;
- no answer is correct.
Question #8
- \(= 1\);
- does not exixt;
- \( = 0\);
- \( = +\infty\);
- no answer is correct.
Question #9
- for any \(\alpha>1\);
- if and only if \(\alpha=1\);
- for a suitable \(\alpha\in(0,1)\);
- never;
- no answer is correct.
Question #10
- \((-\infty,0]\cup[2,+\infty)\);
- \(\mathbb{R}\setminus\{1\}\);
- \([2,+\infty)\);
- \(\mathbb{R}\);
- no answer is correct.
Question #11
- \(\displaystyle \frac{-(\sin x)e^{\cos x}}{e^{\cos x}+1}\);
- \(\displaystyle \frac1{e^{\cos x}+1}\);
- \(\displaystyle \frac{-\sin x}{e^{\cos x}+1}\);
- \(\displaystyle -\sin x\);
- no answer is correct.
Question #12
- in \((-1,+\infty)\);
- in \((-\infty,-2]\) and in \([0,+\infty)\);
- only in \([0,+\infty)\);
- in \((-\infty,-1)\);
- no answer is correct.
Question #13
The function $$f(x)=x^4-2x^3+1$$ has a minimum in
- \(x=0\) and \(x=\frac32\);
- \(x=\frac32\);
- \(x=0\);
- \(x=1\);
- no answer is correct.
Question #14
- \(f(x)=x+x^2+\frac{x^3}2+o(x^3)\);
- \(f(x)=1+2x+\frac{x^2}2+\frac{x^3}6+o(x^3)\);
- \(f(x)=\frac{x^2}2+\frac{x^3}6+o(x^3)\);
- \(f(x)=x+o(x)\);
- no answer is correct.
\(f(x)=x+x^2+\frac{x^3}2+o(x^3)\)
Question #15
- \(= \arctan3-\arctan2\);
- \(= \frac12\ln\frac32\);
- \(= \ln\frac83\);
- \(= 0\);
- no answer is correct.
Question #16
- \(=2\sqrt t+c\), with \(c\in\mathbb{R}\);
- \(=\displaystyle{-\frac2{t^{3/2}}+c}\), with \(c\in\mathbb{R}\);
- \(=\displaystyle{-\frac1{2t^{3/2}}+c}\), with \(c\in\mathbb{R}\);
- \(=\log(\sqrt t)+c\), with \(c\in\mathbb{R}\);
- no answer is correct.
Question #17
- converges if and only if \(\alpha>0\);
- converges if and only if \(\alpha>1\);
- converges for a suitable \(\alpha<0\);
- does not converge for any \(\alpha\in\mathbb{R}\);
- no answer is correct.
Question #18
- converges if and only if \(|x|<1\);
- does not converge for any \(x\in\mathbb{R}\);
- converges if and only if \(x=0\);
- converges for a suitable \(x>1\);
- no answer is correct.
Question #19
- \(\not\exists A^{-1}\);
- \(2, 3\) are eigenvalues of \(A\) and \(\mathbf v_2=(1,-1), \mathbf v_3=(0,1)\) are two corresponding eigenvectors;
- \(A\) is not diagonalizable;
- \(1, 3\) are eigenvalues of \(A\) and \(\mathbf v_1=(1,0), \mathbf v_3=(0,1)\) are two corresponding eigenvectors;
- no answer is correct.
Question #20
- \(1, 2+i, 2-i\) are eigenvalues of \(A\);
- \(1, 1, 3\) are eigenvalues of \(A\);
- \(A\) is diagonalizable in \(\mathbb{R}\);
- \(\text{det}(A)=0\) (\(\text{det}\) stands for the determinant of \(A\));
- no answer is correct.
Exercise #1
In the first integral we use the change of variable \(t=\sqrt[3]{x-2}\), so that \(x=2+t^3\). Hence,
$$\int\frac{x}{\sqrt[3]{x-2}}\, dx=\int\big(6t+3t^4\big)\, dt=3t^2+\frac35t^5+C=3(x-2)^{2/3}+\frac35(x-2)^{5/3}+C=F(x)+C,\quad\text{with \(C\in\mathbb{R}\)},$$
implying
$$\int_{1}^{2}\frac{x}{\sqrt[3]{x-2}}\, dx=F(2)-F(1)=-3+\frac35=-\frac{12}5.$$
In the second integral we use the change of variable \(t=\tan x\), so that
$$\int\frac{\sqrt{\tan x}-1}{\cos^2 x}\, dx=\int\big(\sqrt{t}-1\big)\, dt=\frac23t^{3/2}-t+C=\frac23(\tan x)^{3/2}-\tan x+C=F(x)+C,$$
hence
$$\int_0^{\pi/4}\frac{\sqrt{\tan x}-1}{\cos^2 x}\, dx=F(\pi/4)-F(0)=\frac23-1=-\frac13.$$
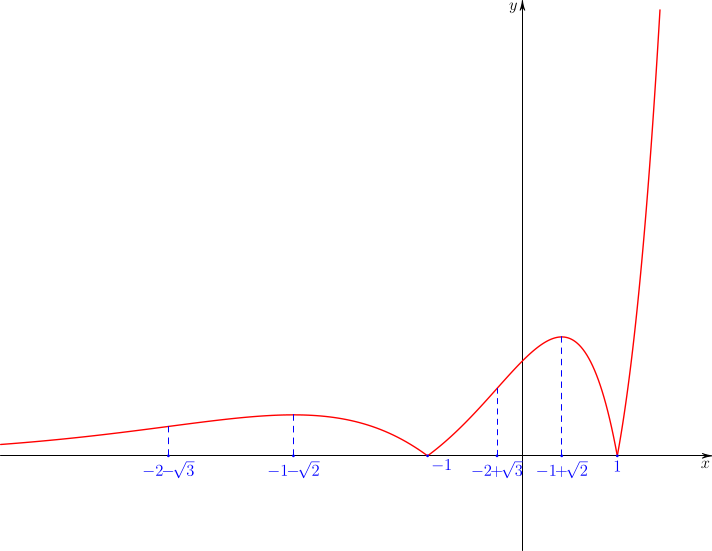
Exercise #2
Study the function
$$f(x)=|x^2-1|e^x$$
and plot a qualitative graph of \(f\).
Exercise #3
Find the Taylor expansion of order \(3\) at \(x=0\) of the function
$$f(x)=e^{x-x^3}-\cos(\sin x).$$
and calculate the limit
$$\lim_{x\to0}\frac{e^{x-x^3}-\cos(\sin x)-x-x^2}{\ln(1+x^3)}.$$
Exercise #4
For which \(x \in \mathbb{R}\) does the series
$$\displaystyle {\sum _{n=1}^{+\infty} \frac {1}{n}}\left(\frac{x}{3}\right)^n\,$$
converge?
Notice that
$$\lim_{n\to\infty}\frac {1}{n}\left(\frac{x}{3}\right)^n=0
\qquad\text{if and only if}\qquad \left|\frac{x}{3}\right|\leq1\qquad\text{if and only if}
\qquad -3\leq x\leq3.$$
So, if \(x<-3\) or \(x>3\), the series does not converge.
Let us analyze the absolute converge of the series if \(-3\leq x\leq 3\). Since
$$\lim_{n\to+\infty}\frac{|a_{n+1}|}{|a_n|}=\lim_{n\to+\infty}\frac {1}{n+1}\left|\frac{x}{3}\right|^{n+1}\frac{n}{\left|\frac{x}{3}\right|^{n}}
=\lim_{n\to+\infty}\frac {n}{n+1}\left|\frac{x}{3}\right|=\left|\frac{x}3\right|.$$
Then, if \(x\in(-3,3)\), the series converges.
If \(x=3\), then \(a_n=\frac1n\), so the series diverges.
If \(x=-3\), then \(a_n=(-1)^n\frac1n\), so by Leinbiz criterion the series converges.
Finally: the series converges if and only if \(-3\leq x<3\).
Exercise #5
Find the plane \(\pi\) passing through \(O=(0,0,0)\) and \(A=(0,-1,1)\), and parallel to the line \(r\) with equation
$$\left\{\begin{array}{l}
x=t\\
y=-t\\
z=1
\end{array}\right.,\qquad \,t\in\mathbb R.$$
Exercise #6
- Find \(k\) such that \(\textbf{v}=(1,1,1)^T\) is an eigenvactor of \(A_k\).
- For such a \(k\), find a basis for \(\mathbb{R}^3\) made by eigenvectors of \(A_k\).